Висота трикутника: Як правильно її обчислити та використовувати в геометрії

Висота трикутника є одним із ключових елементів у вивченні геометрії. Вона не тільки допомагає в обчисленні площі трикутника, але й відіграє важливу роль у різних геометричних задачах. У цій статті ми детально розглянемо поняття висоти трикутника, методи її обчислення, практичне використання, а також декілька прикладів.

Що таке висота трикутника?

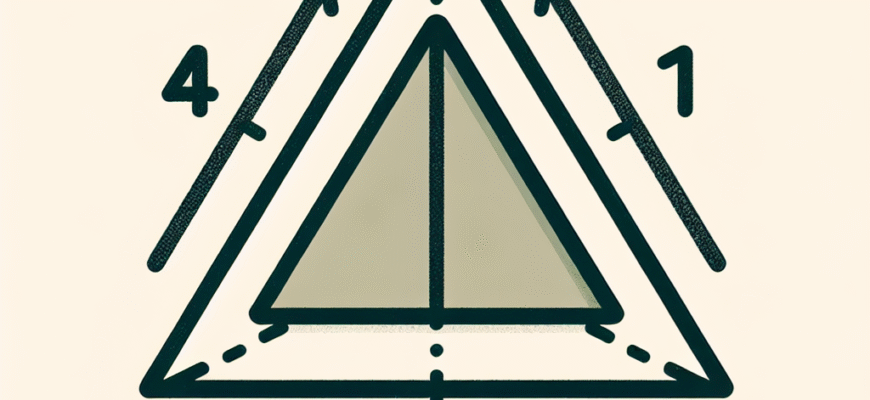
Висота трикутника — це перпендикулярна лінія, проведена з вершини трикутника до протилежної сторони (основи) або до продовження цієї сторони. Вона завжди вимірюється у одиницях довжини, таких як сантиметри або метри.

Основні компоненти висоти:

• Основи трикутника — сторона, до якої проводиться висота.
• Вершина — точка, з якої відводиться висота.

Види трикутників та їх особливості

Трикутники поділяються на три основні типи:

• Рівносторонні трикутники — всі сторони та кути рівні.
• Рівнобедрені трикутники — дві сторони однакові, а кути при основі рівні.
• Різносторонні трикутники — всі сторони і кути різні.

Висота у різних типах трикутників

Тип трикутника	Висота	Взаємозв’язок з основою
Рівносторонній	Висота ділить основи навпіл	Висота дорівнює ( \frac{\sqrt{3}}{2}a )
Рівнобедрений	Перпендикуляр з вершини до основи	Висота ділить основу на дві частини
Різносторонній	Обчислюється за формулою	Висота залежить від конкретних вимірювань

Як обчислити висоту трикутника?

Метод 1: За формулою площі

Одним з найбільш поширених способів обчислення висоти трикутника є використання формули площі. Площа трикутника (S) може бути виражена так:

[ S = \frac{1}{2} a h ]

де:

• ( a ) — довжина основи,
• ( h ) — висота трикутника.

Кроки обчислення:

1. Знайдіть площу трикутника з відомими формулами, або використовуючи методи, наприклад, через сторони.
2. Перепишіть формулу у вигляді висоти:

[ h = \frac{2S}{a} ]

1. Підставте відомі значення у формулу та обчисліть висоту.

Метод 2: З використанням тригонометрії

Висота трикутника також може бути обчислена за допомогою тригонометричних функцій. Для трикутника з відомими кутиками:

• Якщо відомий один з кутів ( \alpha ) і протилежна йому сторона ( a ):

[ h = a \cdot \sin(\alpha) ]

Приклад:

Розглянемо трикутник з гіпотенузою 10 см і кутом 30°.

1. Знайдемо висоту:

[ h = 10 \cdot \sin(30°) = 10 \cdot 0.5 = 5 \, \text{см} ]

Метод 3: Висота в рівнобедреному трикутнику

Для рівнобедреного трикутника, щоб знайти висоту, можна також скористатися формулою:

[ h = \sqrt{b^2 – \left(\frac{a}{2}\right)^2} ]

де:

• ( b ) — довжина сторони,
• ( a ) — основа.

Приклад:

Припустимо, що ( a = 6 \, \text{см} ) і ( b = 5 \, \text{см} ):

[ h = \sqrt{5^2 – \left(\frac{6}{2}\right)^2} = \sqrt{25 – 9} = \sqrt{16} = 4 \, \text{см} ]

Використання висоти трикутника в практиці

Висота трикутника виконує багато практичних функцій. Вона використовується в архітектурі, геодезії, а також у топографії.

Геометричні задачі

1. Обчислення площі: Висота є одним із основних компонентів у формулі площі.
2. Розв’язування тригонометричних задач: Висота часто використовується для обчислення сторін трикутника.
3. Моделювання: У багатьох наукових і технічних задачах.

Приклад задачі:

Скільки квадратних сантиметрів площа трикутника з базою 10 см і висотою 4 см?

Розв’язок:

[ S = \frac{1}{2} 10 4 = 20 \, \text{см}^2 ]

Підсумок

Висота трикутника — це важливий концепт у геометрії, що допомагає в розв’язуванні різноманітних задач. Поєднуючи знання з тригонометрії та математичних розрахунків, ми можемо легко обчислити висоту будь-якого трикутника. Розуміння висоти також значно полегшує завдання в практиці, від архітектури до інженерії.

Ключові моменти для запам’ятовування:

• Висота — це перпендикуляр, проведений від вершини до основи.
• Для обчислення висоти можна використовувати формули площі або тригонометрію.
• Висота грає важливу роль у різноманітних практичних завданнях.

Додаткові ресурси

Для глибшого вивчення теми ви можете скористатися наступними ресурсами:

• Книги з геометрії для учнів.
• Відеоуроки на платформах, таких як YouTube.
• Онлайн-курси з математики на ресурсах, таких як Coursera чи Khan Academy.

Сподіваємося, ця стаття допомогла вам зрозуміти важливість висоти трикутника, та розкрила вам різні методи її обчислення!